2025 SDG 7th biweekly report

Review of the past two weeks

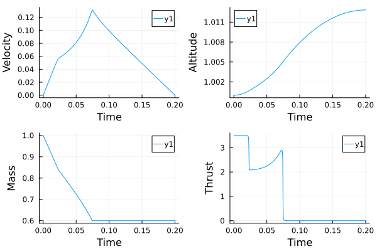
During the last two weeks, I finally get the optimal control interface in BoundaryValueDiffEq.jl working, the previous problem with the sparse hessian of the Lagrangian is caused by the inappropriate intial guess.

The optimal solution of this rocket problem by solving using BoundaryValueDiffEq.jl is as follow:

using BoundaryValueDiffEqMIRK, OptimizationMOI, Ipopt
h_0 = 1                      # Initial height
v_0 = 0                      # Initial velocity
m_0 = 1.0                    # Initial mass
m_T = 0.6                    # Final mass
g_0 = 1                      # Gravity at the surface
h_c = 500                    # Used for drag
c = 0.5 * sqrt(g_0 * h_0)    # Thrust-to-fuel mass
D_c = 0.5 * 620 * m_0 / g_0  # Drag scaling
u_t_max = 3.5 * g_0 * m_0    # Maximum thrust
T_max = 0.2                  # Number of seconds
T = 1_000                    # Number of time steps
Δt = 0.2 / T;                # Time per discretized step

tspan = (0.0, 0.2)
drag(x_h, x_v) = D_c * x_v^2 * exp(-h_c * (x_h - h_0) / h_0)
g(x_h) = g_0 * (h_0 / x_h)^2
function rocket_launch!(du, u, p, t)
    # u_t is the control variable (thrust)
    x_v, x_h, x_m, u_t = u[1], u[2], u[3], u[4]
    du[1] = (u_t-drag(x_h, x_v))/x_m - g(x_h)
    du[2] = x_v
    du[3] = -u_t/c
end
function rocket_launch_bc!(res, u, p, t)
    res[1] = u(0.0)[1] - v_0
    res[2] = u(0.0)[2] - h_0
    res[3] = u(0.0)[3] - m_0
    res[4] = u(0.2)[4] - 0.0
end
cost_fun(u, p) = -u[end - 2] #Final altitude x_h. To minimize, only temporary, need to use temporary solution interpolation here similar to what we do in boundary condition evaluations.
#cost_fun(sol, p) = -sol(0.2)[2]
u0 = [v_0, h_0, m_T, 3.0]
rocket_launch_fun = BVPFunction(rocket_launch!, rocket_launch_bc!; cost = cost_fun, f_prototype = zeros(3))
rocket_launch_prob = BVProblem(rocket_launch_fun, u0, tspan; lb = [0.0, h_0, m_T, 0.0],
    ub = [Inf, Inf, m_0, u_t_max])
sol = solve(rocket_launch_prob, MIRK4(; optimize = Ipopt.Optimizer()); dt = Δt, adaptive=false)

The solution is identical to the solution from JuMP.jl or InfiniteOpt.jl.

TODOs in next two weeks

In the following two weeks, there are a few TODOs:

1. Finalize the interface for optimal control problems, including the interpolation in cost functions, FIRK and Shooting method for optimal control problem and more docs.
2. Finalize a suitable convention for the cost function in formulating optimal control problems, mainly about the interpolating and integral of control variables.